“经济数学”课程标准
课程名称: |
经济数学 |
课程代码: |
01009 |
课时数: |
60 |
适用专业: |
1.经济管理类 |
开设学期: |
1-2 |
一、课程概述
1.课程性质
《经济数学》经济管理类专业的一门必修的公共基础课。
2.课程定位
本课程的开设旨在培养和提升经济管理类专业学生进行专业学习和终生学习所必需的理论知识和数学思维。通过本课程的学习,使学生初步掌握必需、够用的数学理论知识、方法以及培养学生的逻辑思维能力、科学理论理解能力、解决相关专业问题的能力和继续深造的自主学习能力,同时通过Matlab软件的学习为今后的复杂计算提供快捷的方法等。本课程在各专业的课程体系中居于基础服务性地位,主要为后续相关课程肩负着“专业基本素质”中的“经济活动分析”的任务,为各专业课程教学提供必要的数学准备。
3.课程目标
(一)知识目标:
使学生熟练掌握重要的数学概念、定理、公式、方法、思想,即:
(1)理解并熟练掌握:函数与常用经济函数、极限、连续与间断、导数与微分、矩阵、线性方程组、投入产出基本原理、线性规划等概念,理解其几何意义及经济意义;
(2)熟练掌握并会正确使用极限计算公式与方法、导数计算公式和求法、极值与最值求法、边际值与弹性值求法、曲线凹凸性与拐点判定方法、矩阵运算方法、线性方程组的解法、投入产出数学模型的建立与分析等;
(3)掌握常用数学思想,包括:函数思想、转化思想、数形结合思想、极限思想、变化率思想、最优化思想、微元法思想、线性分析思想、定量定性分析思想、建模思想等思想;
(4)会利用MATLAB进行数值计算、符号运算、计算极限、求函数导数、图形处理、最优化问题求解、线性方程(组)求解、矩阵运算、线性规划模型求解。
(二)能力目标:
(1)培养建模能力:使学生能将经济问题量化成数学问题,并会用数学知识和方法求其解;
(2)培养计算能力:使学生具有简单问题的手工计算能力、复杂问题的软件使用能力;
(3)培养数学实验能力:使学生会使用数学工具软件Matlab,通过上机可以完成各种计算,为教学目标的实现扫清障碍;
(4)培养数学方法在经济领域中的应用能力(核心能力):使学生会应用数学知识求解相应经济问题,并会对相应经济问题的计算结果,正确进行数量分析,使后续课程教学顺畅;即会应用函数、极限、导数、积分、投入产出数学模型等求解相关经济问题,并会根据计算结果进行分析、推断、预测;
(5)培养迁移能力:使学生会把数学思想迁移并应用到相关课程的学习中,进行数学问题分析、经济问题分析或其他课程领域等实际问题的分析。
(三)体现创新创业、课程思政和校训精神教育目标。
培养学生具有抽象思维能力、推理能力、想象能力,比较熟练的软件运算能力和综合运用所学知识去提出问题、分析问题和解决问题的能力的同时使其树立正确的价值观,寓道于教、寓德于教、寓教于乐。借助知识点、数学史、典故等,将知识传授与价值引领相结合,引导学生正确做人做事做学问,助力学生的全面发展。将思想政治教育贯穿人才培养全过程,满足学生成长发展需求和期待,实现全过程育人、全方位育人;将“家国共担、手脑并用”的校训文化精神贯穿人才培养全过程,实现以文化人、以文育人。
二、课程设计思路
1.课程设计理念
本课程学习内容的制定依据以学习基础知识为向导,以服务专业为已任,以典型案例为基点,综合理论知识和实践操作为一体的模块化思路设计,把该课程概括为:初等知识模块、微分模块、线性规划模块三大模块,每一模块以典型案例为中心,再讲解学习涉及的数学基础知识,最后回归到用软件来解决案例的繁锁计算,以达到让学生学会运用数学知识解决实际问题。
(2)“客房的定价问题”案例讲授初等函数、极限、Matlab的理论知识,初步使学生掌握初等函数分析能力、Matlab的实际操作能力、计算能力、实际问题的解决能力。由“最优价格模型”案例讲授函数导数、极值、最值、微分、Matlab编程操作知识,使学生掌握求导、微分、求极值的基本方法,掌握实际问题的分析、编程、操作和应用推广能力。以“线性规划生产计划问题”案例为例讲述行列式、矩阵投入产出模型、线性规划模型的基础知识,初步培养学生的分析、计算、编程和解决实际问题的能力。通过三个案例的学习、实践,以达到培养学生数学思想迁移并应用到相关课程的学习中,进行数学问题分析、经济问题分析。
2.课程内容设计思路
序号 |
案例名称 |
案例内容 |
案例成果 |
知识、能力和素质目标 |
1 |
客房的定价问题 |
一住房租赁公司有50套公寓要出租。当租金定为每月180元时,公寓会全部租出去,当租金每月增加10元时,就有一套公寓租不出去,而租出去的房子每月需花费20元的整修维护费。(1)建立总收入与租金之间的数学模型。(2)当房租定多少可获得最大收入? |
为宾馆提供客房制定合理价格 |
知识:函数、常用经济函数、函数的连续性与间断 能力:将经济问题量化成数学问题,并会用数学知识和方法求其解; 素质:知识应用能力、问题解决能力 |
2 |
最优价格模型 |
考虑产销平衡状态下的最优价格问题,利润是销售收入与生产支出之差.已知每件产品的成本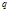 是固定的,在市场竞争的情况下售量 是固定的,在市场竞争的情况下售量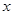 依赖于价格.一般 依赖于价格.一般 是 是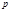 的减函数.试确定价格 的减函数.试确定价格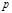 ,使总利润最大(此时的价格称为最优价格) ,使总利润最大(此时的价格称为最优价格) |
中小型商店制定合理的销售策略 |
知识:导数、复合函数 微分、一阶导数的应用 能力:学生会应用数学知识求解相应经济问题,并会对相应经济问题的计算结果,正确进行数量分析 素质:培养思维、推理、表达、创新、探索能力 |
3 |
线性规划生产计划问题 |
某农户计划用12公顷耕地生产玉米,大豆和地瓜,可投入48个劳动日,资金3600元。生产玉米1公顷,需6个劳动日,资金360元,可获净收入2000元;生产1公顷大豆,需6个劳动日,资金240元,可获净收入1500元;生产1公顷地瓜需2个劳动日,资金18元,可获净收入12000元,问怎样安排才能使总的净收入最高。 |
农户制定春种秋收争取最大利益方案 |
知识:行列式、矩阵、线性规划。 能力:培养分析问题、应用软件解决实际问题。 素质:培养学生学会运用数学思想和方法和数学软件的分析、解决问题的动手能力。 |
注:1.①可以是大案例一案到底,也可以是小案例群;②选取的案例要能支撑课程目标的实现;③大案例能够分解成多个有逻辑关系的小案例;④案例群中的各案例之间要有一定的逻辑关系,或并列或包含。
1. 知识、能力和素质目标体现创新创业、课程思政和校训精神教育目标。
一、课程内容结构与课时分配
案例序号 |
案例名称 |
案例内容 |
实践任务 |
实践成果 |
课时 |
理论基础(知识点) |
课时 |
创新创业、课程思政、校训精神教育内容(教学形式或方法) |
1 |
客房的定价问题 |
1.1问题分析、相关变量设置 |
1.1.1 Matlab软件介绍 |
通过客房定问题分析解决房价与出租之间的关系,并非线性关系 |
2 |
函数、常用经济函数 极限的运算、两个重要极限 函数的连续性与间断点 |
10 |
学生礼仪、校圆文化 |
1.2问题分析并提炼相关数学关系(房价与房屋出租这间的关系) |
1.2.1 Matlab软件的符号运算 |
2 |
函数的连续性与拔苗助长的故事 :违反事物的客观规律,急于求成。 |
1.3建立问题的数学模型 |
1.3.1 Matlab软件的数值运算与求导 |
2 |
数列极限与圆周率:讲述刘徽发现割圆术。 |
1.4模型进行求解 |
|
|
2 |
最优价格模型问题 |
2.1针对问题进行分析,作出合理假设 |
2.1.1 Matlab描绘函数图形 |
对本问题分析、借助软件,提高了学生分析问题和实际操作能力,绘图、求导、极值。 |
4 |
导数的概念与定义、导数的经济意义 求导法则、函数求导的基本公式 ★ 复合函数求导 ▲ 高阶导数与微分 微分方程 微分中值定理、一阶导数的应用 |
16 |
|
2.2找出销售量、价格、销售因子、利润之间的模型 |
2.2.1 Matlab软件复合函数的建立、求导、极值问题 |
4 |
极值:题《西林壁》这首诗引入让学生感悟,人生就像连绵不断的曲面,起起落落是必经之路 |
2.3对利润表达式求导、最优解 |
2.3.1 Matlab软件解代数方程与符号微分方程的求解 |
2 |
3 |
线性规划生产计划问题 |
3.1分析问题中生产利润与产品的关系、计划与产品之间的关系 |
3.1.1 Matlab应用行列式、矩阵的运算 |
学生掌握线性规划模型建立、求解、动手操作能力。 |
4 |
行列式的概念及展开 行列式的性质、矩阵的概念及运算 ▲ 线性方程的矩阵解法 线性规划模型 ▲ 线性规划中的投入产出模型 |
10 |
|
3.2确定决策变量(定义),确定目标函数 |
3.2.利用Matlab求解线性规划模型 |
|
3.3写出目标函数与约束条件 |
|
|
3.4求出最优解并进行检验 |
3.4.1生产计划、运输、营养搭配问题 |
4 |
|
3.5对问题进行检验 |
|
|
小计课时 |
24 |
36 |
总计课时 |
30 |
30 |
注: (0)案例——本方案中包含项目之意,编制时可根据课程设计的具体方法明确是案例还是项目即可;选取的案例或项目应有一定的逻辑关系,或并列或包含或递进。
(1)案例内容——意指对案例的分解。
(2)实践任务——意指对完成案例内容相应工作的任务分解和主要技能拓展;
(3)理论基础——意指完成实践任务所必需、够用的知识认知与知识运用,必要时可适度拓展;
(4)符号说明——★:指与实践任务匹配的必需、够用的知识点;
▲:指根据需要可适度拓展的知识点。
(1)创新创业、课程思政、校训精神教育内容根据课程实际情况设计,至少2次内容以上,明确教育内容和教学形式(方法)。
三、考核项目及评价标准
1.过程考核
过程考核包含课堂考核、平时表现与综合过程考核三部分:(1)课堂考核指对应教学任务书中考核内容的考核情况(一学期对每个学生至少有两次以上的考核情况记载);(2)平时表现指学生出勤、上课纪律、课堂参与度和课后作业完成情况等;(3)综合过程考核指对全班学生同时实施的过程考核项目,与下表所列考核项目相对应。
序号 |
考核项目 |
分值比例 |
评价标准 |
优 |
良 |
合格 |
1 |
平时表现 |
20 |
仪表端装、待人礼貌、全出勤、无迟到、早退上课纪律好、课堂积极参 |
仪表端装、待人礼貌、出勤基本到、偶无迟到、早退上课纪律好、课堂积极参 |
仪表端装、待人礼貌、无故旷课二次以内,基本完成课堂作业 |
2 |
课堂考核 |
10 |
积极参与课堂、积极完成老师的提问题和练习,且准确率高,并积极帮助不会的同学 |
参与课堂问答、回答问题表现好 |
能全程参与,在老师和同学的帮助下完成课堂考核项目 |
3 |
综合过程考核项目一 |
10 |
100-85(函数练习) |
84-75 |
74-60 |
4 |
综合过程考核项目一 |
20 |
100-85(极限测试) |
84-75 |
74-60 |
5 |
综合过程考核项目二 |
20 |
100-85(导数、积分测试) |
84-75 |
74-60 |
6 |
综合过程考核项目三 |
20 |
对线性规划作出合理假设、分析、能准确利用软件求出函数的最值、销售量、价格、销售因子、利润之间的模型 |
对线性规划作出基本假设、分析、能准确利用软件求出函数的最值、销售量、价格、销售因子、利润之间的模型 |
在老师、同学帮助下作出假设、分析、能准确利用软件求出函数的最值、销售量、价格、销售因子、利润之间的模型 |
注:(1)考核项目指相应案例内容关注的重点;
(2)评价标准要明确相应创新创业、课程思政、校训精神教育内容的评价标准。
(或用以下表格:
注:(1)考核项目指相应案例内容关注的重点;
(2)要明确相应创新创业、课程思政、校训精神教育内容的评价标准。
2.综合考核
建议本课程综合考核采用理论(或(和)实操)、闭卷(或开卷)方式,综合考核内容依据本课程案例库综合拟定,有关操作程序按教务处相关规定执行。
3.成绩评定
过程考核60%,综合考核40%(比例可根据课程情况设定,每班课程成绩应呈正态分布)。
四、课程资源
1.教材及参考资料(书写格式:作者.教材名[M].出版社,出版时间.)
[1]、朱焕桃.《数学建模教程》.北京理工大学出版社.2013.8
[2]、冯翠连.《应用经济数学》.高等教育出版社. 2008(6)
[3]、裴东林.《经济数学》(上、下).北京邮电大学出版社.2009(12)
[4]、王德才.《应用经济数学》.高等教育出版社. 2008(6)
[4]、季霏.《经济应用数学》.高等教育出版社. 2012(12)
[5]、张钟德《高职Matlab精简实训》.吉林大学出版社.2016.7
2.教学视频
3.其他课程资源(如:学习网站等)
标准执笔人:张钟德 标准审核人:
管理院部:基础课教研部
定稿日期: 2019 年 3月 25 日